It is because,

2 is a positive integer. Likewise, if the square root of any positive integer is also a positive integer, then the first integer is said to be a perfect square.
If

where ‘x’ and ‘y’ both are positive integers, then x is a perfect integer. 1, 4, 9, 16, 25, are some examples for perfect integers.

where ‘x’ and ‘y’ both are positive integers, then x is a perfect integer. 1, 4, 9, 16, 25, are some examples for perfect integers.
How to define the term Surd?
Surd is an irrational number or numerical term involving the radical sign ( ). Further, this is not true/valid only for square root. This is valid for any power with the radical sign. That means it is valid for cube root(
). Further, this is not true/valid only for square root. This is valid for any power with the radical sign. That means it is valid for cube root( ), fourth root (
), fourth root ( ) and so on. The important fact is that the whole numerical value including the radical sign must be irrational if it is to be a Surd.
) and so on. The important fact is that the whole numerical value including the radical sign must be irrational if it is to be a Surd.
Entire Surd is a special instance of Surds, where the number inside the radical sign should have perfect squares as its factors. For example,
if
is considered, 12 is not a perfect square. But,
if
is considered, 12 is not a perfect square. But,
12 = 4 x 3
Where 4 is a perfect square and it is there as a factor of 12 inside the square root. In such a case, these are called as entire surds. These two concepts of surd and entire surds are important in mathematics for several situations. Some of them can be shown with the following examples as below.
- To easier the simplification/calculationExample in figure 1 below
Figure 1 - To get the accurate/correct answerExample in figure 2 below
Figure 2
If there is an entire surd, it is not the simplest way of a surd. Thus, in such cases, it should be simplified to obtain the exact similar value in the form of
 where ‘a’ is a rational number and
where ‘a’ is a rational number and
is an irrational number (surd, where b does not have perfect square factors).
is an irrational number (surd, where b does not have perfect square factors).
Everyone should have good practice in simplification of surds and entire surds. Following are some examples.
Following Figure 3 shows some more lengthy calculations involving Surds and Entire Surds.
 | |||
| Figure 3 |
Hope this may be helpful to you. Contact WitCentre via contact form for anything to clarify or get written what you want. Thanks for reading. Have a good day!



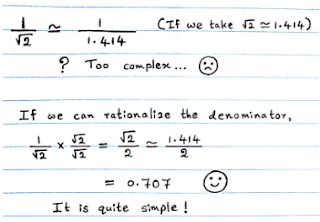
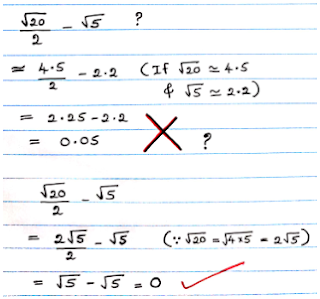







Post A Comment:
0 comments: